Ryan P. Creedon | Ph.D. in Applied Mathematics
A warm welcome to all! I’m a Prager Assistant Professor and NSF Postdoc Fellow at Brown University, where I study instabilities in water and other geophysical fluids.
About
I study nonlinear waves in geophysical fluids, with particular emphasis on water waves big and small! I use a combination of numerical modeling, asymptotic methods, and rigorous mathematical analysis to detect coherent structures in geophysical fluids and their potential instabilities. Of recent interest to me are instabilities present in the oceans’ mixed layer, which have implications on how the atmosphere and ocean interact with each other on various spatiotemporal scales.
Teaching is another core aspect of my work. I have five years of experience as an instructor at the University of Washington, where I received the Boeing Teaching Award in 2020, 2021, and 2023. I also have 10 years of professional tutoring experience through organizations such as Penn State Learning, the Making Connections program at the University of Washington, and the Bellevue Learning Center. Below you’ll find some of my teaching resources and best practices that I use in my classrooms.

Professional Appointments
- Mathematical Sciences Postdoctoral Research Fellow (MSPRF), National Science Foundation, 2024-2027.
- Prager Assistant Professor, Division of Applied Mathematics at Brown University, 2024-2027.
- Acting Instructor, Department of Applied Mathematics at University of Washington, 2022-2024.
Education
- Ph.D., Department of Applied Mathematics at University of Washington, 2022.
- M.S., Department of Applied Mathematics at University of Washington, 2017.
- M.S., Department of Meteorology and Atmospheric Science at Penn State University, 2016.
- B.S., Department of Meteorology and Atmospheric Science at Penn State University, 2016.
- B.S., Department of Mathematics at Penn State University, 2016.
Research
If there’s one thing we know for sure about waves, it is that they are ubiquitous. At all scales of motion in the universe, you can find waves, and in any area of natural science, you can find someone who studies some type of wave. Though much of my research concerns water waves specifically, many of the questions I ask and techniques I use can be extrapolated to any kind of wave in a geophysical fluid of interest. These questions include: what are the equations that govern the behavior of the wave, what properties do these equations have, how do we find solutions of these equations, and in what sense are these solutions stable or unstable?
Current Projects
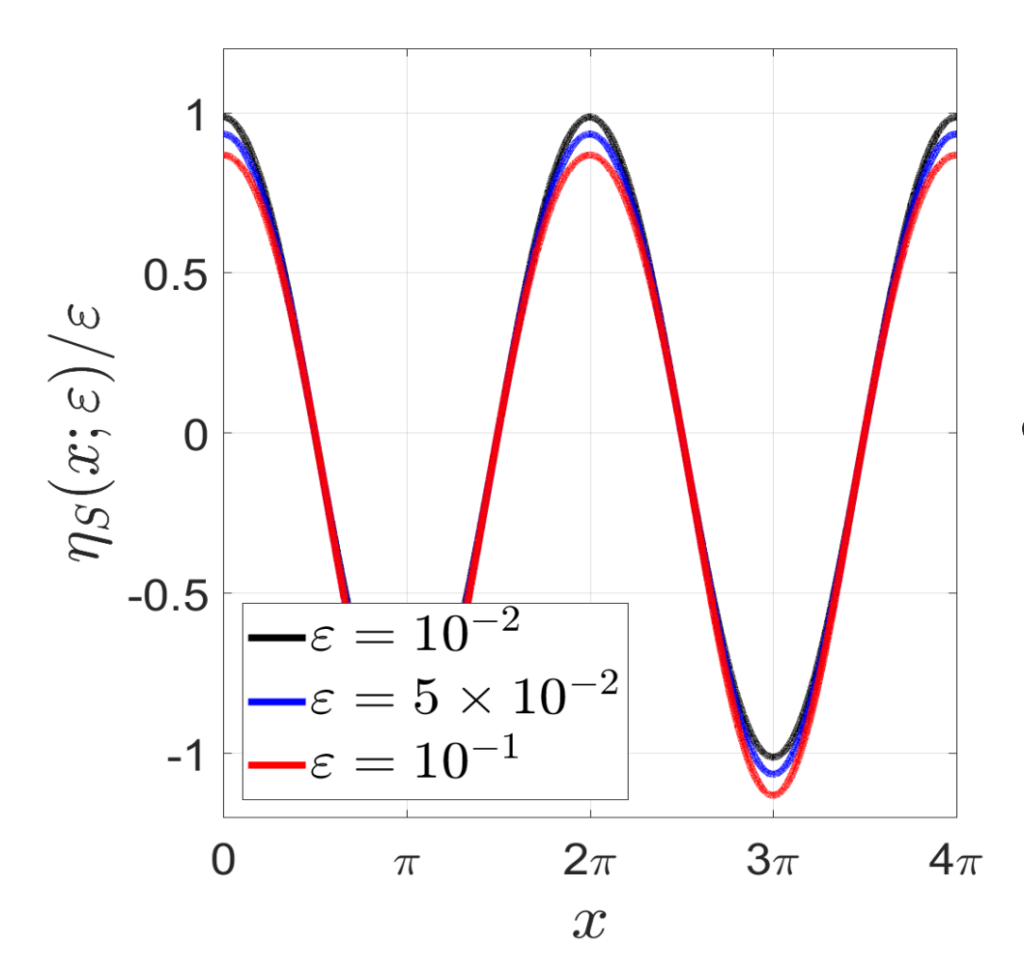
Asymptotic and Heuristic Models of Water Waves
- The KdV Family of Equations
- Boussinesq-Whitham Systems
- Elliptic and Soliton Solutions
- Integrability of Equations
- Nonlinear Stability of Solutions
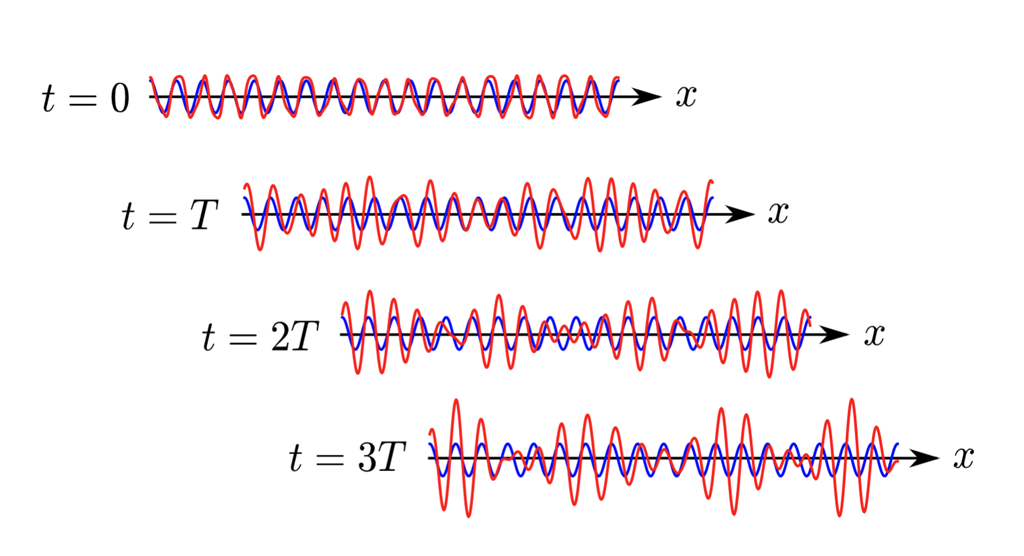
Instabilities of Non-Linear Water Waves
- Stokes Wave Expansions
- Resonant Wave Interactions
- Spectral Stability of Stokes Waves
- Longitudinal and Transverse Instabilities
- Inclusion of Surface Tension and Other Effects
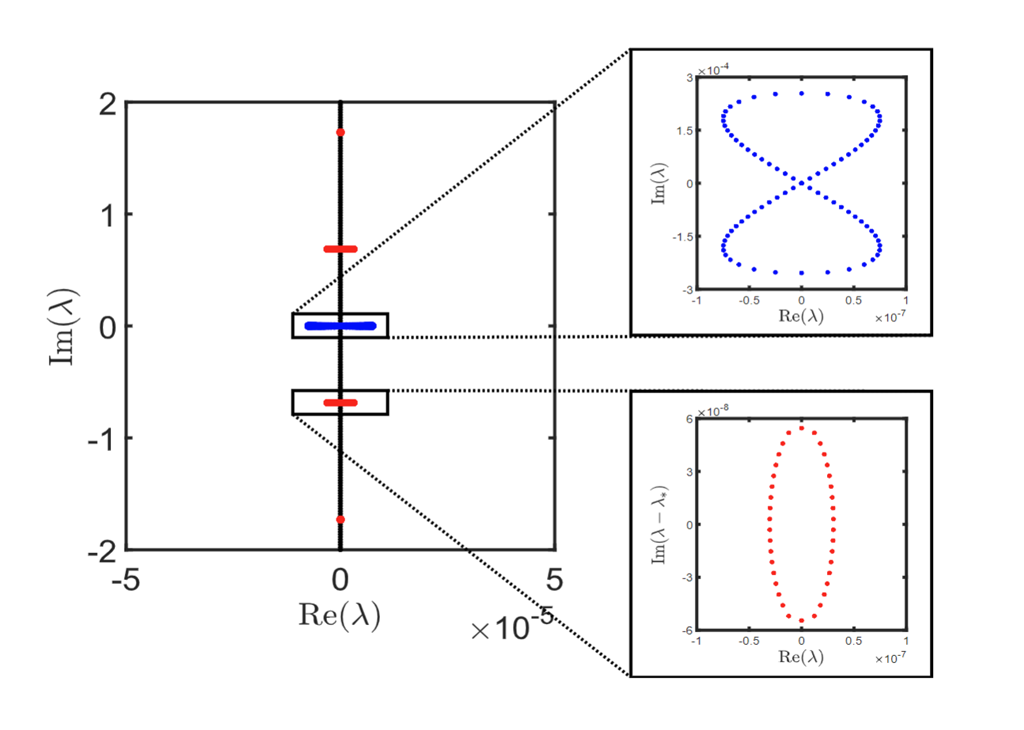
Computing Spectra of Linear Operators
- Properties of Discrete and Continuous Spectra
- Asymptotic Behavior of Spectral Elements
- Numerical Computation of Spectral Elements
- Behavior of Eigenfunctions
- Squared Eigenfunction Connection
Publications
7. Creedon, R. P., Nguyen, H. Q., & Strauss, W. A. (2024). Proof of the transverse instability of Stokes waves at finite depth. Submitted to SIAM Journal on Mathematical Analysis.
6. Creedon, R. P., Nguyen, H. Q., & Strauss, W. A. (2024). Stokes waves are unstable, even very small ones. Submitted to EMS Surveys in Mathematical Sciences.
5. Creedon, R. P., Nguyen, H. Q., & Strauss, W. A. (2023). Proof of the transverse instability of Stokes waves. Accepted to Annals of Partial Differential Equations.
4. Creedon, R. P., & Deconinck, B. (2023). A high-order asymptotic analysis of the Benjamin–Feir instability spectrum in arbitrary depth. Journal of Fluid Mechanics, 956, A29.
3. Creedon, R. P., Deconinck, B., & Trichtchenko, O. (2022). High-frequency instabilities of Stokes waves. Journal of Fluid Mechanics, 937, A24.
2. Creedon, R. P., Deconinck, B., & Trichtchenko, O. (2021). High-frequency instabilities of a Boussinesq– Whitham system: a perturbative approach. Fluids, 6(4), 136. [Cover Story]
1. Creedon, R. P., Deconinck, B., & Trichtchenko, O. (2021). High-frequency instabilities of the Kawahara equation: a perturbative approach. SIAM Journal on Applied Dynamical Systems, 20(3), 1571-1595.
Teaching
Many of my teachers and professors had lasting impacts on my personal and professional development, and I can only hope to return the favor one day.
Below you will find information about the courses I’ve taught as well as an assortment of teaching materials that I hope to grow in the years to come.

TBD
Amath 301: Beginning Scientific Computing
Spring 2024
Amath 353: Partial Differential Equations and Waves
Spring 2024
Amath 352: Applied Linear Algebra and Numerical Analysis
Winter 2024
Cfrm 405: Mathematical Methods for Quantitative Finance
Fall 2023
Amath 301: Beginning Scientific Computing
Spring 2023
Amath 352: Applied Linear Algebra and Numerical Analysis
Winter 2023
Amath 383: Introduction to Continuous Mathematical Modeling
Fall 2022
Amath 352: Applied Linear Algebra and Numerical Analysis
Winter 2022
Amath 353: Partial Differential Equations and Waves
Summer 2021
Amath 353: Partial Differential Equations and Waves
Spring 2021
Amath 352: Applied Linear Algebra and Numerical Analysis
Winter 2020
Amath 353: Partial Differential Equations and Waves
Summer 2019
Teaching Resources
Contact
Email: ryan_creedon@brown.edu
Brown University
Division of Applied Mathematics
182 George St.
Room 205
Providence, RI 02906

